日本不卡一区视频-日本不卡视频一区二区三区-日本不卡视频一区二区-日本不卡高清免费v日本-色国产视频

有關正弦交流電的三種表示方法，分別是解析法，正弦曲線法，旋轉矢量法，正弦交流電表示方法，用于表現正弦交流電的瞬時值隨時間變化的規律。

正弦交流電的表示方法

用于表現正弦交流電的瞬時值隨時間變化的規律。

1、解析法

解析法是用數學公式表述正弦交流電與實踐變化關系的方法。

公式如下：

e=Emsin(ωt+Φe)

u=Umsin(ωt+Φu)

i=Imsin(ωt+Φi)

它可以表達正弦量的最大值、初相角和周期。

由上述公式可知，只要知道一個正弦量的最大值，初相角和頻率，一個正弦量即完整的被確定，通常把最大值、初相角、角頻率叫做正弦交流電的三要素。

2、正弦曲線法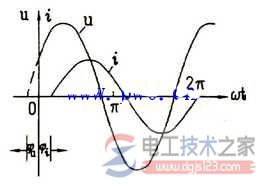

正弦曲線圖示法即利用平面直角坐標系中的橫坐標表示時間t，縱坐標表示正弦量的瞬時值，并根據解析式的計算，用繪制出的正弦曲線圖來表達正弦量的方法，如右圖所示。

3、旋轉矢量法

正弦交流電還可以用旋轉矢量法表示。

什么是旋轉矢量？

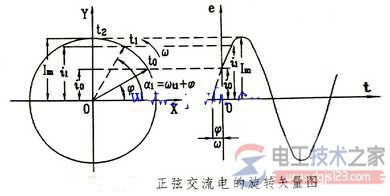
如圖，從原點出發作一有向線段，令它的長度等于正弦量的最大值Im，與水平軸的夾角等于正弦量的初相位Φ，并以等于正弦量角頻率的角速度ω逆時針旋轉，則在任一瞬間，該有向線段在縱軸上的投影就等于該正弦量的瞬時值Imsin(ωt+Φ)。這樣的有向線段就叫做旋轉矢量。

正弦交流電的電壓、電流和電動勢都可以用旋轉矢量表示，要進行同頻率正弦量的加減運算時，可以先做出各個正弦量對于的旋轉矢量，然后按照平行四邊形法則求出合成旋轉矢量，這合成旋轉矢量的長度就是總的正弦量的最大值，合成旋轉矢量與軸OX(橫軸)的夾角就是總正弦量的初相位。

從上右圖中可知，用旋轉矢量來表示正弦量通常是很繁瑣的，一般情況下：

只用有向線段的初始位置(t=0的位置)來表示正弦量，即吧有向線段的長度表示為正弦量的大小，把有向線段與橫軸正向的夾角表示正弦量的初相位，這種表示正弦量的方法叫做相量法。

如果使有向線段的長度等于正弦量的最大值，這種相量稱為正弦量的最大值相量，以符號Em、Um、Im表示。

在實際問題中，我們遇到的往往是正弦量的有效值，如果使用有向線段的長度等于正弦量的有效值，這種相量叫做有效值相量，用符號U、E、I表示。

幾個同頻率的相量畫在同一個相量圖中，可以按矢量合成的方法對相量進行加減運算。